Bienvenidos a todos a este blogger de matemáticas

Bienvenidos chicos y chicas, en este blog explicaremos y entenderemos  diversas cosas sobre la matemática donde aprenderemos la suma de logaritmos, raíces y las semejanzas.

Intrducción:

¿que son los logaritmos?

Un logaritmo es un  exponente el cual es necesario elevar a a una determinada cantidad 

para que resulte un número.

¿que son las raíces?

Raíz es una cantidad x que se puede multiplicar por sí misma una o más veces para que salga un numero determinad
Pero para encontrar esa cantidad que se multiplica se recurre a la operación de extraer la raíz a partir del número y esto se utiliza usando el símbolo √, que se llama radical.

¿que son las semejanzas?

Son 2 figuras semejantes cuando tienen la misma forma pero eso no quiere decir que poseen el mismo tamaño. Es decir, una de las figuras es una ampliación o una reducción de la otra. 
 los ángulos determinan la forma y las longitudes el tamaño

logaritmos:

el logaritmo de un numero,es el exponente al cual se debe elevar la base para obtener un numero

un logaritmo de x en base a es igual a y pero debe cumplir con la condición general de que a (la base) sea mayor que cero y a la vez distinta que uno  

        

                                                                     

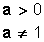
para decirlo de una forma mas simple un logaritmo es solo una forma de expresar una potencia.

un ejemplo de un logaritmo es:

log (8- 4x )- log (3-2x) = 2 <-------------se aplican 
log (8-4x ) - log (3-2x) = 2             propiedades de logaritmos.
      log( 8-4x/ 3-2x) = 2                          
       8-4x/3-2x= 10^2= 100
         196x=292
           x= 292/192=73/49

Propiedades de los logaritmos

No existe el logaritmo de un número con base negativa.

No existe el logaritmo de un número negativo.

No existe el logaritmo de cero.

El logaritmo de 1 es cero.

El logaritmo de a en base a es uno.

El logaritmo en base a de una potencia en base a es igual al exponente.

                 
 aquí un vídeo para que entiendan 

raíces:

La raíz consiste en encontrar la base de la potencia conociendo el exponente (que en la raíz se llama índice) y la cantidad subradical. 

Los nombres de las partes que constituyen cada operación matemática son
X:  Base de la potencia          
  X:   Valor de la raíz
n:  Exponente de la potencia              
 n:   Índice de raíz
 a:  Valor de la potencia                           
  a:   Cantidad subradical (o radicando)

                 
                 Ejemplo:  

                                 

                                   

semejanzas:

como se decía en la introducción una semejanza Son 2 figuras semejantes cuando tienen la misma forma pero no necesariamente el mismo tamaño. Es decir, una de las figuras es una ampliación o una reducción de la otra. 

Normalmente los ángulos determinan la forma y las longitudes el tamaño

Cuando la semejanza es entre objetos, la misma puede ser en cuanto a tamaño, color o forma. Por ejemplo, “el color del automóvil del vecino es semejante al de mi amigo jose”. 

 Veamos un ejercicio :

EJERCICIO  : En una fotografía, María y Frenando miden 2,5 cm y 2,7 cm, respectivamente; en la realidad, María tiene una altura de 167,5 cm. ¿A qué escala está hecha la foto? ¿Qué altura tiene Fernando en la realidad? 

Solución 

* Calculamos la escala: Altura en la foto de María=   2,5 =    1

                                       -------------------------------      ------   ---

                                      Escala Altura real de María=167,5=  67 

* La escala es 1:67. 

 * Calculamos la altura real de Fernando: Altura real = 67 · 2,7 =180,9 cm

Para analizar:

¿De que nos sirve aplicar logaritmos en nuestra vida?

•  la Economía y la Banca: en los índices de crecimiento también se aplica en la demanda y en la oferta
•  la Estadística: de vez en cuando suele aplicarse en el indice de la población.
•  la Publicidad: Se realizan las estadísticas sobre la campaña publicitaria , también cuando se realizan cálculos matemáticos con logaritmos. 
•  la Medicina: esto se aplica  en ciertos fenómenos  como el resultado de experimentos psicológicos. También se aplica en la inmunología.
•  la Ingeniería Civil: Cuando se resuelven problemas específicos,  teniendo en cuenta una ecuación de segundo grado.
•  la Biología:  En los estudios de los efectos nutricionales de los organismos. 
•  la Geología: Sirven de cálculo, para calcular la intensidad de un evento
•  la Astronomía: sirve Para determinar la magnitud estelar de una estrella o planeta.
•  la Química: Para calcular el PH de las sustancias se utilizan logaritmos. 
•  la Topografía: cuando queremos saber la altura de un edificio usando la base y el ángulo.
• la Música: El pentagrama es una escala logarítmica, además ayuda a medir los grados de tonalidad ya que se pueden representar por el logaritmo en base 2.

¿De que nos sirve aplicar raíces en nuestras vidas?

Realmente aplicar esto en la vida diaria es falso pero si te ayuda a aprender nuevos métodos matemáticos y así tener mayor conocimiento de la matemática en si 

¿De que nos sirve aplicar semejanzas en nuestras vidas?

la semejanza la encontramos hasta en las personas, semejante rostro, altura etc también en objetos

 la semejanza también ayuda a los pintores para poder dibujar un objeto de magnitudes grandes a  menor altura y similares rasgos .

                                                            Conclusión

A medida de que e hecho el blog no solo aprendí a calcular logaritmos raíces y semejanzas si no que también me ayudo a mira como esos simples cálculos pueden emplearse en la vida cotidiana.Montones de veces uno se pregunta de que nos sirven las matemáticas relativamente avanzas que nos pasan pero si nos ponemos a analizar e investigar descubrimos que si nos sirven quizás no las empleamos a menudo pero están.

fuentes:

*Ejerccicio sacado de - slideshare.net Remove 

*texto estudiantil matemática segundo medio

*profesor en linea
*rinconmatematico
*yahoo respuestas (jaja)
*youtube